Álgebra computacional con Maxima
Maxima es un sistema de algebra computacional. Esto es un software que proporciona un entorno interactivo y de programación para la manipulación matemática a nivel simbólico y numérico.
Herramientas tan conocidas como Mapple o Mathematica basaron su sintáxis en Maxima que fué implementado por William F. Schelter en Common Lisp. Maxima se inspira en el sistema algebráico computerizado más antiguo del mundo: MACSYMA desarrollado en el MIT. Maxima es software libre distribuido bajo la licencia GPL.
1. Instalando Maxima
Maxima es software libre y está empaquetado para las principales distribuciones de GNU/Linux, así que no necesitamos más que buscar e instalar los paquetes maxima y texmacs. Este último para utilizar acceder a Maxima desde Texmacs de manera que se cuenta con una visualización más pulida.
2. Iniciando una sesión en Maxima
Se puede utilizar Maxima como un programa independiente desde la línea de comandos:
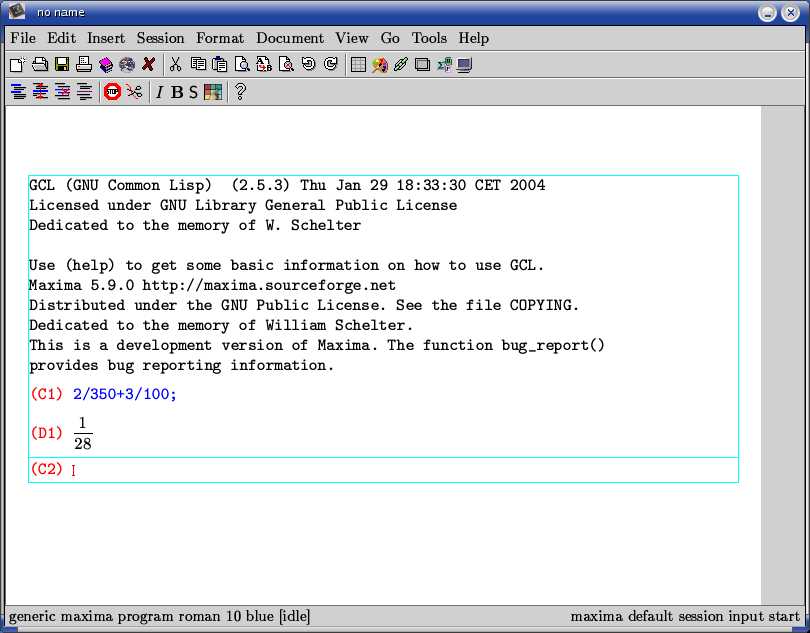
O desde la interfaz gráfica de TeXmacs:
El funcionamiento de Maxima es sencillo, el usuario introduce un comando y el programa proporciona una salida. Por eso, a cada entrada del usuario se asigna una etiqueta Cn y a cada resultado una Dn (Display). El número permite referirse a la entrada o al resultado posteriormente.
En Maxima no se realiza distinción entre mayúsculas y minúsculas salvo para los nombres de las variables. Para finalizar cada entrada se debe escribir un carácter ; o bien un carácter $, aunque en este caso no se presenta la visualización del resultado.
3. Algunas cosas a tener en cuenta:
- Si desea referir algún resultado, no es necesario que lo vuelva a escribir, simplemente escriba la etiqueta asociada a tal resultado o comando.
- Si desea referir el resultado generado por la orden inmediatamente anterior, se puede usar o bien la etiqueta D asociada a tal comando o el símbolo de porcentaje
%. - Las constante e (Euler), i (unidad imaginaria) y π están representadas por
%E(ó%e),%I(ó%i) y%PI(ó%pi). - Para asignar valores a las variables se utilizan los dos puntos
:, pues el igual queda reservado para la representación de ecuaciones. - Hay diferentes palabras reservadas que no pueden utilizarse como nombres de variables:
And,At,Diff,Do,Elseif,Elseif,For,From,If,Integrate,Limit,Next,Or,Product,Step,Sum,Then,Thru,Unless,While.
4. Posibilidades
Entre las características de Maxima se encuentra soporte para:
- Álgebra. Manipulación y cálculos simbólicos y analíticos.
- Precisión arbitraria.
- Resolución de sistemas de ecuaciones lineales y no lineales.
- Soporte para números complejos.
- Cálculo Diferencial e Integral (derivadas, integrales, Laplace, Taylor, Fourier...).
- Ecuaciones diferenciales.
- Álgebra matricial.
- Gráficas 2D y 3D.
Referencias: